درخت فنویک (Fenwick Tree)¶
خب رفیق، بیا با هم بریم سراغ درخت فنویک. فرض کن یه تابع به اسم $f$ داریم که یک «عملگر گروهی» (group operator) هست. نگران اسمش نباش، یعنی یه تابع دو ورودیئه که شرکتپذیره (یعنی ترتیب اجراش مهم نیست، مثلاً $(a*b)*c = a*(b*c)$)، یه عضو خنثی داره (مثل صفر برای جمع)، و هر عضوی یه وارون داره (مثل عدد منفی برای جمع). حالا فرض کن یه آرایه از اعداد صحیح به اسم $A$ به طول $N$ هم داریم. برای سادگی، این تابع $f$ رو با علامت $*$ نشون میدیم، یعنی $f(x,y) = x*y$. (چون گفتیم شرکتپذیره، دیگه لازم نیست موقع استفاده از $*$ هی پرانتز بذاریم که ترتیب اجرا رو مشخص کنیم، چون فرقی نداره.)
درخت فنویک یه ساختمان داده خیلی باحاله که:
- مقدار تابع $f$ رو روی یه بازه مشخص $[l, r]$ (یعنی $A_l * A_{l+1} * \dots * A_r$) توی زمان $O(\log N)$ حساب میکنه.
- مقدار یه عضو از آرایه $A$ رو توی زمان $O(\log N)$ آپدیت میکنه.
- حافظهی $O(N)$ میخواد (یعنی به اندازه خود آرایه $A$).
- پیادهسازی و استفادهش خیلی راحته، مخصوصاً وقتی پای آرایههای چندبعدی وسط باشه.
معروفترین کاربرد درخت فنویک، محاسبه جمع یه بازه است. مثلاً اگه عملگرمون همون جمع معمولی (+) روی اعداد صحیح باشه ($f(x,y) = x + y$)، اون وقت علامت $*$ ما همون $+$ میشه و میتونیم چیزایی مثل $A_l + A_{l+1} + \dots + A_{r}$ رو سریع حساب کنیم.
به درخت فنویک، درخت اندیسگذاری شده دودویی (Binary Indexed Tree یا به اختصار BIT) هم میگن. این ساختار داده اولین بار تو مقالهای به اسم «یک ساختار داده جدید برای جداول فراوانی تجمعی» توسط پیتر ام. فنویک (Peter M. Fenwick) در سال ۱۹۹۴ معرفی شد.
توضیحات¶
نمای کلی¶
برای اینکه قضیه راحتتر جا بیفته، فرض میکنیم اون تابع $f$ همون عمل جمع معمولی روی اعداد صحیحه، یعنی $f(x,y) = x+y$.
خب، فرض کن یه آرایه از اعداد صحیح $A[0 \dots N-1]$ بهمون دادن. (حواست باشه که اینجا اندیسها از صفر شروع میشن). درخت فنویک در واقع فقط یه آرایه دیگهست به اسم $T[0 \dots N-1]$ که هر خونهش، یعنی $T_i$، جمع یه تیکه از آرایه $A$ رو تو خودش نگه میداره. مشخصاً، جمع بازه $[g(i), i]$ رو:
اینجا $g$ یه تابعیه که همیشه $0 \le g(i) \le i$ هست. چند خط پایینتر کامل توضیح میدم که این تابع $g$ چیه و چطور کار میکنه.
به این ساختار داده میگن درخت، چون میشه یه نمایش درختی خوشگل ازش کشید، ولی در عمل لازم نیست یه درخت واقعی با گره و یال مدل کنیم. فقط کافیه همین آرایه $T$ رو داشته باشیم تا بتونیم به همهی درخواستها (queries) جواب بدیم.
نکته: درختی که اینجا توضیح میدیم، از اندیسگذاری صفر-پایه (zero-based) استفاده میکنه. خیلیها هم از نسخهای استفاده میکنن که یک-پایه (one-based) هست. برای همین، تو بخش پیادهسازی، یه نسخه جایگزین که از اندیسگذاری یک-پایه استفاده میکنه هم برات گذاشتم. هر دو نسخه از نظر پیچیدگی زمانی و حافظه مثل هم هستن.
حالا میتونیم یه شبهکد برای دوتا عملیات اصلی بنویسیم. کد زیر جمع عناصر $A$ رو تو بازه $[0, r]$ حساب میکنه و یه عنصر $A_i$ رو آپدیت (زیاد) میکنه:
تابع sum(عدد صحیح r):
نتیجه = 0
تا زمانی که (r >= 0):
نتیجه += t[r]
r = g(r) - 1
بازگرداندن نتیجه
تابع increase(عدد صحیح i, عدد صحیح delta):
برای تمام j هایی که g(j) <= i <= j:
t[j] += delta
تابع sum اینجوری کار میکنه:
- اول میاد جمع بازهی $[g(r), r]$ (که همون $T[r]$ هست) رو به
resultاضافه میکنه. - بعد، یهو «میپره» به بازهی $[g(g(r)-1), g(r)-1]$ و جمع اون رو هم به نتیجه اضافه میکنه.
- این کار اونقدر ادامه پیدا میکنه تا از بازههای مختلف بپره و در نهایت از کل محدودهی صفر خارج بشه و حلقه تموم شه.
تابع increase هم با منطق مشابهی کار میکنه، ولی در جهت مخالف، یعنی اندیسها رو زیاد میکنه:
- مقدار
deltaرو به تمام خونههایt[j]اضافه میکنه که بازهشون یعنی $[g(j), j]$ شامل اندیسiباشه. در واقع، این تابع تمام عناصری از $T$ رو آپدیت میکنه که $A_i$ توی بازهشون قرار داره.
پیچیدگی هر دو تابع sum و increase به این بستگی داره که تابع $g$ چطور تعریف شده باشه.
میشه تابع $g$ رو به روشهای مختلفی تعریف کرد.
مثلاً اگه $g(i) = i$ باشه، اون وقت $T = A$ میشه (که در این حالت، پیدا کردن جمع بازه کند میشه).
یا میتونیم $g(i) = 0$ بگیریم. این کار معادل استفاده از آرایههای مجموع پیشوندی (prefix sum) هست (که اینجا پیدا کردن جمع بازه $[0, i]$ خیلی سریعه، ولی آپدیت کردن یه عنصر کند میشه).
قسمت هوشمندانه الگوریتم درخت فنویک، تعریف خاصی از تابع $g$ هست که باعث میشه هر دو عملیات توی زمان $O(\log N)$ انجام بشن.
تعریف ¶
محاسبه g(i) با یه ترفند بیتی باحال انجام میشه:
ما آخرین گروه از بیتهای 1 پشت سر هم در انتهای نمایش باینری i رو به 0 تبدیل میکنیم.
به عبارت دیگه، اگه کمارزشترین بیت i توی مبنای دو، 0 باشه، اون وقت g(i) = i.
وگرنه، کمارزشترین بیت 1 هست و ما این 1 و بقیه بیتهای 1 پشت سر همِ بعد از اون رو برعکس میکنیم.
مثلاً:
خبر خوب اینه که لازم نیست درگیر این منطق بشی، چون یه راه خیلی ساده با عملیات بیتی برای این کار وجود داره:
که اینجا & همون عملگر AND بیتی خودمونه. راحت میتونی خودت رو قانع کنی که این فرمول دقیقاً همون کار بالا رو انجام میده.
حالا فقط باید یه راهی پیدا کنیم که روی همهی اون j هایی که g(j) <= i <= j هستن حرکت کنیم (برای تابع increase).
راحت میشه دید که اگه از i شروع کنیم و هر بار آخرین بیت 0 رو 1 کنیم، میتونیم به همهی این jها برسیم.
اسم این عملیات رو میذاریم h(j).
مثلاً برای i = 10:
و جای تعجب نداره که برای این کار هم یه فرمول بیتی ساده و شیک وجود داره:
که اینجا | همون عملگر OR بیتی هست.
تصویر زیر یه نمایش درختی از فنویک رو نشون میده. گرههای درخت، بازههایی که هر کدوم پوشش میدن رو نمایش میدن.
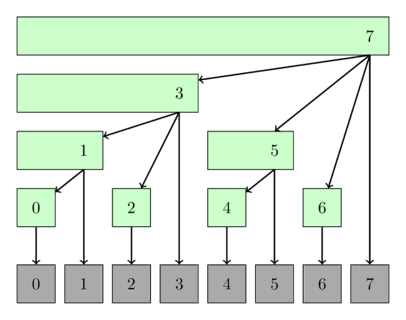
پیادهسازی¶
پیدا کردن جمع در آرایه یکبعدی¶
اینجا کد یه درخت فنویک رو میبینی که برای پیدا کردن جمع بازهها و آپدیت کردن یه عنصر خاص به کار میره.
درخت فنویک استاندارد فقط میتونه جمع بازههایی از نوع $[0, r]$ رو با تابع sum(int r) حساب کنه، ولی ما میتونیم با یه ترفند ساده، جمع هر بازه دلخواه $[l, r]$ رو هم به دست بیاریم: کافیه sum(r) رو حساب کنیم و sum(l-1) رو ازش کم کنیم.
این کار توی تابع sum(int l, int r) انجام شده.
این پیادهسازی دو تا سازنده (constructor) هم داره. میتونی یه درخت فنویک خالی (مقداردهی شده با صفر) بسازی، یا یه آرایه رو بهش بدی تا خودش به فرم فنویک تبدیلش کنه.
struct FenwickTree {
vector<int> bit; // این همون آرایه درخت اندیسگذاری شده دودویی ماست
int n;
// سازنده برای ساختن یه درخت خالی
FenwickTree(int n) {
this->n = n;
bit.assign(n, 0);
}
// سازنده برای ساختن درخت از روی یه آرایه موجود
FenwickTree(vector<int> const &a) : FenwickTree(a.size()) {
for (size_t i = 0; i < a.size(); i++)
add(i, a[i]);
}
// جمع بازه [0, r] رو حساب میکنه
int sum(int r) {
int ret = 0;
for (; r >= 0; r = (r & (r + 1)) - 1)
ret += bit[r];
return ret;
}
// جمع بازه [l, r] رو حساب میکنه
int sum(int l, int r) {
return sum(r) - sum(l - 1);
}
// به عنصر idx مقدار delta رو اضافه میکنه
void add(int idx, int delta) {
for (; idx < n; idx = idx | (idx + 1))
bit[idx] += delta;
}
};
ساخت خطی¶
پیادهسازی بالا برای ساختن درخت از روی یک آرایه به زمان $O(N \log N)$ احتیاج داره. میشه این کار رو سریعتر و در زمان $O(N)$ انجام داد.
ایدهش اینه: مقدار a[i] روی bit[i] تأثیر میذاره. bit[i] هم به نوبهی خودش روی bit[i | (i+1)] (که والدش محسوب میشه) تأثیر میذاره و همینطور زنجیرهوار تا آخر. پس ما میتونیم وقتی آرایه a رو پیمایش میکنیم، هر bit[i] رو که حساب کردیم، تأثیرش رو به والدش منتقل کنیم. اینطوری کل ساختار رو خطی میسازیم.
FenwickTree(vector<int> const &a) : FenwickTree(a.size()){
for (int i = 0; i < n; i++) {
bit[i] += a[i];
int r = i | (i + 1); // پیدا کردن والد
if (r < n) bit[r] += bit[i]; // انتقال تاثیر به والد
}
}
پیدا کردن کمینه بازه در آرایه یکبعدی¶
واضحه که پیدا کردن کمینه یه بازه دلخواه $[l, r]$ با درخت فنویک به این سادگیها نیست، چون درخت فنویک فقط میتونه به درخواستهای نوع $[0, r]$ جواب بده.
علاوه بر این، هر بار که یه مقدار رو update میکنی، مقدار جدید باید حتماً کوچکتر از مقدار فعلی باشه.
این دوتا محدودیت بزرگ به این دلیله که عملگر $min$ روی مجموعه اعداد صحیح، یه «گروه» تشکیل نمیده، چون عناصر وارون (inverse) نداره (مثلاً وارون عمل min(a, 5) چی میتونه باشه؟).
struct FenwickTreeMin {
vector<int> bit;
int n;
const int INF = (int)1e9; // یه عدد خیلی بزرگ به عنوان بینهایت
FenwickTreeMin(int n) {
this->n = n;
bit.assign(n, INF);
}
FenwickTreeMin(vector<int> a) : FenwickTreeMin(a.size()) {
for (size_t i = 0; i < a.size(); i++)
update(i, a[i]);
}
// کمینه بازه [0, r] رو برمیگردونه
int getmin(int r) {
int ret = INF;
for (; r >= 0; r = (r & (r + 1)) - 1)
ret = min(ret, bit[r]);
return ret;
}
// مقدار خونه idx رو با val آپدیت میکنه (اگه val کوچکتر باشه)
void update(int idx, int val) {
for (; idx < n; idx = idx | (idx + 1))
bit[idx] = min(bit[idx], val);
}
};
توجه: البته میشه یه درخت فنویک پیادهسازی کرد که هم بتونه کمینه بازه دلخواه رو پیدا کنه و هم آپدیتهای دلخواه رو انجام بده. مقاله Efficient Range Minimum Queries using Binary Indexed Trees همچین روشی رو توضیح میده. ولی تو اون روش باید یه درخت فنویک دیگه هم کنارش داشته باشی و پیادهسازیش خیلی سختتر از نسخه معمولی برای جمعه.
پیدا کردن جمع در آرایه دوبعدی¶
همونطور که قبلاً گفتم، بردن درخت فنویک به ابعاد بالاتر خیلی راحته.
struct FenwickTree2D {
vector<vector<int>> bit;
int n, m;
// init(...) { ... }
// جمع مستطیل از (0,0) تا (x,y)
int sum(int x, int y) {
int ret = 0;
for (int i = x; i >= 0; i = (i & (i + 1)) - 1)
for (int j = y; j >= 0; j = (j & (j + 1)) - 1)
ret += bit[i][j];
return ret;
}
// اضافه کردن delta به خونه (x,y)
void add(int x, int y, int delta) {
for (int i = x; i < n; i = i | (i + 1))
for (int j = y; j < m; j = j | (j + 1))
bit[i][j] += delta;
}
};
رویکرد اندیسگذاری از یک¶
برای این روش، تعریف $T[]$ و $g()$ رو یه کم تغییر میدیم. اینجا میخوایم $T[i]$ جمع بازه $[g(i)+1, i]$ رو نگه داره. این کار پیادهسازی رو یه کم عوض میکنه ولی در عوض فرمولهای بیتیش خیلی خوشگل و متقارن میشن.
تابع sum(عدد صحیح r):
نتیجه = 0
تا زمانی که (r > 0):
نتیجه += t[r]
r = g(r)
بازگرداندن نتیجه
تابع increase(عدد صحیح i, عدد صحیح delta):
برای تمام j هایی که g(j) < i <= j:
t[j] += delta
محاسبه g(i) اینجا اینطوری تعریف میشه:
آخرین بیت 1 رو در نمایش باینری i خاموش (toggle) کن.
آخرین بیت 1 رو میشه با i & (-i) استخراج کرد (این یه ترفند معروف تو برنامهنویسی مسابقاته). پس فرمول g این شکلی میشه:
و برای آپدیت هم باید توی دنبالهی $i,~ h(i),~ h(h(i)),~ \dots$ حرکت کنیم که h(i) اینطوری تعریف میشه:
همونطور که میبینی، مزیت اصلی این روش اینه که عملیات بیتی sum و add خیلی شبیه و مکمل هم میشن.
کد زیر رو میتونی مثل بقیه پیادهسازیها استفاده کنی، ولی حواست باشه که داخلش از اندیسگذاری یک-پایه استفاده میکنه.
struct FenwickTreeOneBasedIndexing {
vector<int> bit; // درخت اندیسگذاری شده دودویی
int n;
FenwickTreeOneBasedIndexing(int n) {
this->n = n + 1;
bit.assign(n + 1, 0);
}
FenwickTreeOneBasedIndexing(vector<int> a)
: FenwickTreeOneBasedIndexing(a.size()) {
for (size_t i = 0; i < a.size(); i++)
add(i, a[i]);
}
int sum(int idx) {
int ret = 0;
// اندیس رو یکی زیاد میکنیم تا با سیستم 1-based مچ بشه
for (++idx; idx > 0; idx -= idx & -idx)
ret += bit[idx];
return ret;
}
int sum(int l, int r) {
return sum(r) - sum(l - 1);
}
void add(int idx, int delta) {
// اندیس رو یکی زیاد میکنیم
for (++idx; idx < n; idx += idx & -idx)
bit[idx] += delta;
}
};
عملیات روی بازهها¶
یه درخت فنویک میتونه این عملیاتهای بازهای رو هم پشتیبانی کنه:
- آپدیت نقطهای و پرسوجوی بازهای
- آپدیت بازهای و پرسوجوی نقطهای
- آپدیت بازهای و پرسوجوی بازهای
۱. آپدیت نقطهای و پرسوجوی بازهای¶
این همون درخت فنویک معمولی خودمونه که بالاتر کامل توضیح دادیم.
۲. آپدیت بازهای و پرسوجوی نقطهای¶
با یه ترفند ساده، میتونیم عملیات برعکس رو هم انجام بدیم: یعنی یه بازه رو با یه مقداری جمع کنیم و بعد مقدار یه نقطه خاص رو بپرسیم.
فرض کن درخت فنویک ما اولش همهش صفره.
حالا فرض کن میخوایم بازه $[l, r]$ رو به اندازه x زیاد کنیم.
ترفندش اینه: دو تا آپدیت نقطهای روی درخت فنویک انجام میدیم: add(l, x) و add(r+1, -x).
حالا اگه بخوایم مقدار $A[i]$ رو پیدا کنیم، کافیه جمع پیشوندی تا i رو با همون تابع sum معمولی حساب کنیم.
بیا ببینیم چرا این درسته. وقتی مقدار A[i] رو میخوایم، سه حالت پیش میاد:
* اگه $i < l$ باشه، هیچکدوم از اون دو تا آپدیت روی جمع تا i تأثیر نذاشتن، پس جواب میشه ۰ (که درسته).
* اگه $i \in [l, r]$ باشه، آپدیت اول یعنی add(l, x) تأثیرش رو میذاره و جواب میشه x (که درسته).
* اگه $i > r$ باشه، آپدیت دوم یعنی add(r+1, -x) میاد و اثر آپدیت اول رو خنثی میکنه، پس جواب دوباره ۰ میشه (که باز هم درسته، چون ما فقط مقدار اضافهشده رو حساب میکنیم).
پیادهسازی زیر از اندیسگذاری یک-پایه استفاده میکنه.
void add(int idx, int val) {
for (++idx; idx < n; idx += idx & -idx)
bit[idx] += val;
}
void range_add(int l, int r, int val) {
add(l, val);
add(r + 1, -val);
}
int point_query(int idx) {
int ret = 0;
for (++idx; idx > 0; idx -= idx & -idx)
ret += bit[idx];
return ret;
}
توجه: البته اگه بخوای فقط یه نقطه A[i] رو زیاد کنی، میتونی از range_add(i, i, val) استفاده کنی.
۳. آپدیت بازهای و پرسوجوی بازهای¶
برای اینکه هم آپدیت بازهای داشته باشیم و هم پرسوجوی بازهای، از دو تا BIT به اسمهای $B_1[]$ و $B_2[]$ استفاده میکنیم که اولش همهشون صفرن.
فرض کن میخوایم بازه $[l, r]$ رو به اندازه مقدار $x$ زیاد کنیم.
مثل روش قبلی، دو تا آپدیت نقطهای روی $B_1$ انجام میدیم: add(B1, l, x) و add(B1, r+1, -x).
و یه سری آپدیت هم روی $B_2$ انجام میدیم. الان میگم چیه.
def range_add(l, r, x):
add(B1, l, x)
add(B1, r+1, -x)
add(B2, l, x*(l-1))
add(B2, r+1, -x*r)
حالا قسمت جادویی ماجرا اینه که چطور با این دو تا BIT، جمع پیشوندی تا اندیس i رو حساب کنیم. فرمولش اینه:
شاید اولش عجیب به نظر برسه، ولی بیا با هم ببینیم چرا کار میکنه. بعد از اینکه بازه $[l, r]$ رو با $x$ آپدیت کردیم، جمع پیشوندی sum[0, i] باید این مقادیر رو بده:
حالا بیا ببینیم فرمول ما چی بهمون میده:
اگه عبارتها رو ساده کنی، میبینی که دقیقاً همون مقادیر مورد نیاز ما رو تولید میکنه! در واقع $B_2$ به ما کمک میکنه که جملههای اضافی که از ضرب sum(B1, i) * i به وجود میاد رو خنثی کنیم.
برای پیدا کردن جمع یه بازه دلخواه $[l, r]$ هم کافیه prefix_sum(r) رو حساب کنیم و prefix_sum(l-1) رو ازش کم کنیم.
# N: اندازه آرایه
# B1, B2: دو تا آرایه BIT ما
def add(b, idx, x):
while idx <= N:
b[idx] += x
idx += idx & -idx
def range_add(l, r, x):
add(B1, l, x)
add(B1, r+1, -x)
add(B2, l, x * (l - 1))
add(B2, r+1, -x * r)
def sum(b, idx):
total = 0
while idx > 0:
total += b[idx]
idx -= idx & -idx
return total
def prefix_sum(idx):
return sum(B1, idx) * idx - sum(B2, idx)
def range_sum(l, r):
return prefix_sum(r) - prefix_sum(l-1)
مسائل تمرینی¶
- UVA 12086 - Potentiometers
- LOJ 1112 - Curious Robin Hood
- LOJ 1266 - Points in Rectangle
- Codechef - SPREAD
- SPOJ - CTRICK
- SPOJ - MATSUM
- SPOJ - DQUERY
- SPOJ - NKTEAM
- SPOJ - YODANESS
- SRM 310 - FloatingMedian
- SPOJ - Ada and Behives
- Hackerearth - Counting in Byteland
- DevSkill - Shan and String (archived)
- Codeforces - Little Artem and Time Machine
- Codeforces - Hanoi Factory
- SPOJ - Tulip and Numbers
- SPOJ - SUMSUM
- SPOJ - Sabir and Gifts
- SPOJ - The Permutation Game Again
- SPOJ - Zig when you Zag
- SPOJ - Cryon
- SPOJ - Weird Points
- SPOJ - Its a Murder
- SPOJ - Bored of Suffixes and Prefixes
- SPOJ - Mega Inversions
- Codeforces - Subsequences
- Codeforces - Ball
- GYM - The Kamphaeng Phet's Chedis
- Codeforces - Garlands
- Codeforces - Inversions after Shuffle
- GYM - Cairo Market
- Codeforces - Goodbye Souvenir
- SPOJ - Ada and Species
- Codeforces - Thor
- CSES - Forest Queries II
- Latin American Regionals 2017 - Fundraising