مجموعههای مجزا (Disjoint Set Union)¶
تو این مقاله قراره با هم ساختمان دادهی مجموعههای مجزا یا DSU رو بررسی کنیم. خیلی وقتها بهش Union Find (ادغام-پیدا کردن) هم میگن، چون دو تا کار اصلیاش همینهاست.
ببین، این ساختمان داده کارای زیر رو برامون انجام میده. فرض کن یه سری عنصر داریم که هر کدومشون توی یه مجموعهی جدا از هم قرار گرفتن. DSU به ما یه عملیات برای ادغام کردن دو تا مجموعه میده و همچنین میتونه بهمون بگه که یه عنصر خاص توی کدوم مجموعه قرار داره. نسخهی کلاسیکش یه کار سوم هم انجام میده: میتونه با یه عنصر جدید، یه مجموعهی تکعضوی جدید بسازه.
پس، رابط کاربری اصلی این ساختمان داده از سه تا عملیات ساده تشکیل شده:
make_set(v)- یه مجموعهی جدید میسازه که فقط شامل عنصرvهست.union_sets(a, b)- دو تا مجموعهی مشخص شده رو با هم ادغام میکنه (یعنی مجموعهای کهaتوشه و مجموعهای کهbتوشه).find_set(v)- نماینده (که بهش لیدر هم میگن) مجموعهای که عنصرvتوش قرار داره رو برمیگردونه. این نماینده، یکی از عنصرهای خود اون مجموعه است. اینکه کی لیدر باشه رو خود ساختمان داده انتخاب میکنه (و ممکنه در طول زمان، مخصوصاً بعد از فراخوانیunion_sets، تغییر کنه). از این نماینده میتونیم استفاده کنیم تا ببینیم دو تا عنصر توی یه مجموعه هستن یا نه.aوbدقیقاً توی یه مجموعه هستن، اگر و فقط اگرfind_set(a) == find_set(b). اگه اینطور نباشه، یعنی توی مجموعههای متفاوتی قرار دارن.
همونطور که جلوتر با جزئیات بیشتری توضیح میدم، این ساختمان داده بهت اجازه میده هر کدوم از این عملیاتها رو به طور میانگین توی زمان تقریباً $O(1)$ انجام بدی.
راستی، تو یکی از بخشها، یه ساختار جایگزین برای DSU رو هم توضیح میدیم که پیچیدگی میانگینش یکم کندتره و $O(\log n)$ هست، ولی در عوض میتونه از DSU معمولی قویتر باشه.
ساخت یک ساختمان داده کارآمد¶
ایده اینه که مجموعهها رو به شکل یه سری درخت ذخیره کنیم: هر درخت نمایندهی یه مجموعه است. و ریشهی هر درخت، نماینده یا همون لیدر اون مجموعه خواهد بود.
تو عکس زیر میتونی یه نمونه از این نمایش درختی رو ببینی.
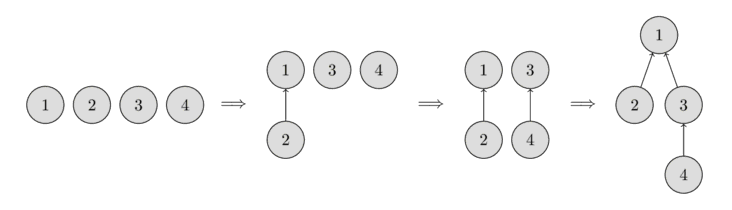
اولش، هر عنصر برای خودش یه مجموعهی جداست، پس هر رأس یه درخت تکگرهایه. بعد، مجموعهای که عنصر ۱ توشه رو با مجموعهای که عنصر ۲ توشه ادغام میکنیم. بعدش، مجموعهی عنصر ۳ رو با مجموعهی عنصر ۴ ادغام میکنیم. و در آخر، مجموعهی عنصر ۱ رو با مجموعهی عنصر ۳ یکی میکنیم.
برای پیادهسازی این ایده، باید یه آرایهی parent داشته باشیم که برای هر عنصر، به والد مستقیمش توی درخت اشاره میکنه.
پیادهسازی ساده¶
خب، بیا با هم اولین پیادهسازی DSU رو بنویسیم. اولش خیلی ناکارآمد و کُنده، ولی نگران نباش، بعداً با دو تا بهینهسازی خفن، کاری میکنیم که هر فراخوانی تقریباً در زمان ثابت انجام بشه.
همونطور که گفتیم، کل اطلاعات مربوط به مجموعهها توی یه آرایه به اسم parent نگهداری میشه.
برای ساختن یه مجموعهی جدید (عملیات make_set(v)), خیلی ساده یه درخت با ریشهی v درست میکنیم، یعنی والد v رو خود v قرار میدیم.
برای ادغام دو تا مجموعه (عملیات union_sets(a, b)), اول لیدر مجموعهی a و لیدر مجموعهی b رو پیدا میکنیم.
اگه لیدرها یکی باشن، یعنی اینا از قبل توی یه مجموعه بودن و کاری لازم نیست انجام بدیم.
در غیر این صورت، خیلی راحت میتونیم والد یکی از لیدرها رو اون یکی لیدر قرار بدیم و اینطوری دو تا درخت رو به هم وصل میکنیم.
و در نهایت پیادهسازی تابع پیدا کردن لیدر (عملیات find_set(v)):
خیلی ساده از عنصر v شروع میکنیم و اونقدر پدرهاشو دنبال میکنیم تا به ریشه برسیم؛ یعنی گرهی که والدش خودشه.
این عملیات رو خیلی راحت میشه به صورت بازگشتی پیاده کرد.
void make_set(int v) {
parent[v] = v;
}
int find_set(int v) {
if (v == parent[v])
return v;
return find_set(parent[v]);
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b)
parent[b] = a;
}
ولی خب، این پیادهسازی خیلی کارآمد نیست.
خیلی راحت میشه یه مثال زد که توش درختها تبدیل به زنجیرههای بلند بشن.
تو این حالت، هر فراخوانی find_set(v) میتونه $O(n)$ طول بکشه.
این سرعت، زمین تا آسمون با اون چیزی که ما دنبالشیم (یعنی نزدیک به زمان ثابت) فرق داره. پس بیا دو تا بهینهسازی رو ببینیم که بهمون اجازه میده کار رو به شکل چشمگیری سریعتر کنیم.
بهینهسازی فشردهسازی مسیر (Path compression)¶
این بهینهسازی برای اینه که تابع find_set رو سریعتر کنیم.
ایده اینه: وقتی ما find_set(v) رو برای یه گره مثل v صدا میزنیم، در واقع داریم لیدر p رو برای تمام گرههایی که روی مسیر بین v و خود لیدر واقعی یعنی p قرار دارن، پیدا میکنیم.
ترفند اینه که بیایم والد همهی این گرههایی که سر راهمون دیدیم رو مستقیماً به p وصل کنیم و اینطوری مسیر رو برای همشون کوتاهتر کنیم.
تو عکس زیر میتونی این عملیات رو ببینی.
سمت چپ یه درخت داریم، و سمت راست همون درخت رو بعد از فراخوانی find_set(7) میبینی که مسیرها برای گرههای ۷، ۵، ۳ و ۲ کوتاه شدن.
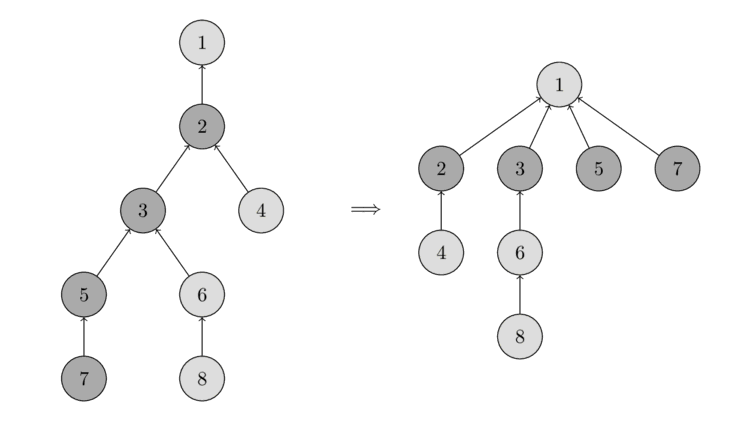
پیادهسازی جدید find_set این شکلی میشه:
int find_set(int v) {
if (v == parent[v])
return v;
return parent[v] = find_set(parent[v]);
}
این پیادهسازی ساده دقیقاً همون کاری رو میکنه که گفتیم: اول لیدر مجموعه (ریشه) رو پیدا میکنه و بعدش موقع برگشت از بازگشتها (stack unwinding)، والد تمام گرههای توی مسیر رو مستقیماً به اون لیدر وصل میکنه.
این تغییر ساده به تنهایی پیچیدگی زمانی رو به طور میانگین به $O(\log n)$ برای هر فراخوانی میرسونه (اثباتش رو فعلاً بیخیال). یه تغییر دیگه هم هست که این رو از این هم سریعتر میکنه.
ادغام بر اساس اندازه / رتبه (Union by size / rank)¶
تو این بهینهسازی، ما عملیات union_set رو تغییر میدیم.
دقیقتر بخوام بگم، ما تصمیم میگیریم که کدوم درخت به اون یکی وصل بشه.
توی پیادهسازی ساده، همیشه درخت دوم به اولی وصل میشد.
این کار در عمل میتونه منجر به ساختن درختهایی با زنجیرههایی به طول $O(n)$ بشه.
با این بهینهسازی، ما با انتخاب هوشمندانهی اینکه کدوم درخت به اون یکی وصل بشه، از این مشکل جلوگیری میکنیم.
روشهای مختلفی برای این کار وجود داره. دو تا از محبوبترینهاشون اینها هستن: تو روش اول، از اندازهی درختها به عنوان «رتبه» استفاده میکنیم و تو روش دوم، از عمق درخت استفاده میکنیم (دقیقتر بگم، یه کران بالا برای عمق، چون با فشردهسازی مسیر، عمق واقعی کمتر میشه).
در هر دو روش، اصل بهینهسازی یکیه: ما همیشه درختی که رتبهی کمتری داره رو به درختی که رتبهی بالاتری داره وصل میکنیم.
این پیادهسازی ادغام بر اساس اندازه است:
void make_set(int v) {
parent[v] = v;
size[v] = 1;
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (size[a] < size[b])
swap(a, b);
parent[b] = a;
size[a] += size[b];
}
}
و این هم پیادهسازی ادغام بر اساس رتبه با استفاده از عمق درخت:
void make_set(int v) {
parent[v] = v;
rank[v] = 0;
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (rank[a] < rank[b])
swap(a, b);
parent[b] = a;
if (rank[a] == rank[b])
rank[a]++;
}
}
پیچیدگی زمانی¶
همونطور که قبلاً گفتم، اگه هر دو بهینهسازی – یعنی فشردهسازی مسیر رو با ادغام بر اساس اندازه/رتبه – ترکیب کنیم، به پرسوجوهایی با زمان تقریباً ثابت میرسیم. معلوم شده که پیچیدگی زمانی سرشکن شده (amortized) نهایی $O(\alpha(n))$ هست، که $\alpha(n)$ معکوس تابع آکرمنه. این تابع خیلی خیلی آهسته رشد میکنه. در واقع اینقدر آهسته رشد میکنه که برای تمام مقادیر منطقی $n$ (مثلاً $n < 10^{600}$) از $4$ بیشتر نمیشه.
پیچیدگی سرشکن شده، یعنی زمان میانگین هر عملیات، وقتی که یه سری عملیات پشت سر هم انجام میدیم. ایده اینه که ما زمان کل یه دنباله از عملیات رو تضمین میکنیم، در حالی که ممکنه یه عملیات خاص خیلی کندتر از زمان سرشکن شده باشه. مثلاً تو مورد ما، یه فراخوانی خاص ممکنه تو بدترین حالت $O(\log n)$ طول بکشه، اما اگه $m$ تا از این فراخوانیها رو پشت هم انجام بدیم، به طور میانگین به زمان $O(\alpha(n))$ میرسیم.
اثبات این پیچیدگی زمانی رو هم نمیاریم، چون خیلی طولانی و پیچیدهست.
راستی، اینم بگم که DSU با ادغام بر اساس اندازه/رتبه، ولی بدون فشردهسازی مسیر، با پیچیدگی $O(\log n)$ برای هر پرسوجو کار میکنه.
اتصال بر اساس اندیس / اتصال با شیر یا خط (Linking by index / coin-flip linking)¶
هم ادغام بر اساس رتبه و هم ادغام بر اساس اندازه، نیاز دارن که برای هر مجموعه یه سری دیتای اضافی ذخیره کنیم و این مقادیر رو تو هر عملیات ادغام، بهروز نگه داریم. یه الگوریتم تصادفی هم وجود داره که عملیات ادغام رو یکم سادهتر میکنه: اتصال بر اساس اندیس.
ایده اینه که به هر مجموعه یه مقدار تصادفی به اسم اندیس اختصاص بدیم و همیشه مجموعهای که اندیس کوچیکتری داره رو به مجموعهای که اندیس بزرگتری داره وصل کنیم. احتمالش زیاده که یه مجموعهی بزرگتر، اندیس بزرگتری هم نسبت به یه مجموعهی کوچیکتر داشته باشه، پس این عملیات خیلی شبیه ادغام بر اساس اندازه عمل میکنه. در واقع میشه ثابت کرد که این عملیات همون پیچیدگی زمانی ادغام بر اساس اندازه رو داره. البته در عمل یه کوچولو از ادغام بر اساس اندازه کندتره.
میتونی اثبات پیچیدگی و حتی تکنیکهای ادغام بیشتری رو اینجا پیدا کنی.
void make_set(int v) {
parent[v] = v;
index[v] = rand();
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (index[a] < index[b])
swap(a, b);
parent[b] = a;
}
}
یه تصور غلط رایج اینه که اگه فقط یه سکه بندازیم تا تصمیم بگیریم کدوم مجموعه به اون یکی وصل بشه، همون پیچیدگی رو به دست میاریم. ولی این درست نیست. مقالهای که بالاتر لینک دادم، حدس میزنه که اتصال با شیر یا خط همراه با فشردهسازی مسیر، پیچیدگی $\Omega\left(n \frac{\log n}{\log \log n}\right)$ داره. و توی بنچمارکها هم عملکردش خیلی بدتر از ادغام بر اساس اندازه/رتبه یا اتصال بر اساس اندیسه.
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (rand() % 2)
swap(a, b);
parent[b] = a;
}
}
کاربردها و بهبودهای مختلف¶
تو این بخش، چند تا از کاربردهای این ساختمان داده رو بررسی میکنیم، هم کاربردهای очевидный و هم یه سری بهبودها برای خود ساختمان داده.
مؤلفههای همبندی در یک گراف¶
این یکی از کاربردهای خیلی واضح DSU هست.
مسئله به طور رسمی اینطوری تعریف میشه: اولش یه گراف خالی داریم. باید بتونیم رأس و یالهای غیرجهتدار بهش اضافه کنیم و به پرسوجوهایی به شکل $(a, b)$ جواب بدیم: "آیا رأسهای $a$ و $b$ توی یه مؤلفه همبندی از گراف قرار دارن؟"
اینجا میتونیم مستقیماً از DSU استفاده کنیم و به یه راهحل برسیم که اضافه کردن یه رأس یا یال و جواب دادن به یه پرسوجو رو به طور میانگین تو زمان تقریباً ثابت انجام میده.
این کاربرد خیلی مهمه، چون تقریباً همین مسئله تو الگوریتم کراسکال برای پیدا کردن درخت پوشای کمینه هم پیش میاد. با استفاده از DSU میتونیم پیچیدگی رو از $O(m \log n + n^2)$ به $O(m \log n)$ بهبود بدیم.
جستجو برای مؤلفههای همبندی در یک تصویر¶
یکی از کاربردهای DSU این مسئله است: یه تصویر $n \times m$ پیکسلی داریم. اولش همهی پیکسلها سفیدن، بعد یه سری پیکسل سیاه میشن. میخوایم اندازهی هر مؤلفه همبندی سفید رو توی تصویر نهایی پیدا کنیم.
برای حلش، خیلی ساده روی تمام پیکسلهای سفید تصویر راه میریم، برای هر سلول چهار تا همسایهش رو چک میکنیم، و اگه همسایه هم سفید بود، union_sets رو صدا میزنیم.
پس ما یه DSU با $nm$ گره داریم که هر کدوم نمایندهی یه پیکسل هستن.
درختهای نهایی توی DSU همون مؤلفههای همبندیای هستن که دنبالشون بودیم.
این مسئله رو میشه با DFS یا BFS هم حل کرد، ولی روشی که اینجا گفتیم یه مزیت داره: میتونه ماتریس رو ردیف به ردیف پردازش کنه (یعنی برای پردازش یه ردیف فقط به ردیف قبلی و ردیف فعلی نیاز داریم، و فقط به یه DSU که برای عناصر یه ردیف ساخته شده). اینطوری حافظه مصرفی $O(\min(n, m))$ میشه.
ذخیره اطلاعات اضافی برای هر مجموعه¶
DSU بهت اجازه میده خیلی راحت اطلاعات اضافی رو برای هر مجموعه ذخیره کنی.
یه مثال ساده، اندازهی مجموعههاست: ذخیره کردن اندازه رو قبلاً تو بخش ادغام بر اساس اندازه توضیح دادیم (اطلاعات توسط لیدر فعلی مجموعه ذخیره میشد).
به همین شکل – با ذخیره کردن اطلاعات تو گرههای لیدر – میتونی هر اطلاعات دیگهای رو هم در مورد مجموعهها نگه داری.
فشردهسازی پرشها در طول یک قطعه / رنگآمیزی زیرآرایهها به صورت آفلاین¶
یکی از کاربردهای باحال DSU اینه: یه سری گره داریم و هر گره یه یال خروجی به یه گره دیگه داره. با DSU میتونی نقطهی پایانی که بعد از دنبال کردن همهی یالها از یه نقطهی شروع خاص بهش میرسیم رو در زمان تقریباً ثابت پیدا کنی.
یه مثال خوب از این کاربرد، مسئله رنگآمیزی زیرآرایهها است. یه قطعه به طول $L$ داریم، هر عنصر اولش رنگ ۰ داره. باید برای هر پرسوجوی $(l, r, c)$، زیرآرایهی $[l, r]$ رو با رنگ $c$ رنگآمیزی کنیم. در آخر میخوایم رنگ نهایی هر سلول رو پیدا کنیم. فرض میکنیم که همهی پرسوجوها رو از قبل میدونیم، یعنی مسئله آفلاینه.
برای حلش، میتونیم یه DSU بسازیم که برای هر سلول، یه لینک به سلول رنگنشدهی بعدی رو نگه داره. پس اولش هر سلول به خودش اشاره میکنه. بعد از رنگ کردن یه قطعه، تمام سلولهای اون قطعه به سلول بعدیِ اون قطعه اشاره میکنن.
حالا برای حل مسئله، پرسوجوها رو برعکس در نظر میگیریم: از آخر به اول. اینطوری وقتی یه پرسوجو رو اجرا میکنیم، فقط لازمه سلولهایی که هنوز توی زیرآرایهی $[l, r]$ رنگ نشدن رو رنگ کنیم. بقیهی سلولها از قبل رنگ نهاییشون رو دارن. برای اینکه سریع روی همهی سلولهای رنگنشده حرکت کنیم، از DSU استفاده میکنیم. چپترین سلول رنگنشده توی یه قطعه رو پیدا میکنیم، رنگش میکنیم و با استفاده از اشارهگر، به سلول خالی بعدی در سمت راستش میپریم.
اینجا میتونیم از DSU با فشردهسازی مسیر استفاده کنیم، ولی نمیتونیم از ادغام بر اساس رتبه/اندازه استفاده کنیم (چون مهمه که بعد از ادغام، کی لیدر میشه). بنابراین پیچیدگی هر ادغام $O(\log n)$ میشه (که البته اونم خیلی سریعه).
پیادهسازی:
for (int i = 0; i <= L; i++) {
make_set(i);
}
for (int i = m-1; i >= 0; i--) {
int l = query[i].l;
int r = query[i].r;
int c = query[i].c;
for (int v = find_set(l); v <= r; v = find_set(v)) {
answer[v] = c;
parent[v] = v + 1;
}
}
یه بهینهسازی هم وجود داره:
میتونیم از ادغام بر اساس رتبه استفاده کنیم، اگه سلول رنگنشدهی بعدی رو توی یه آرایهی اضافی end[] ذخیره کنیم.
اونوقت میتونیم دو تا مجموعه رو بر اساس هیوریستیکهاشون ادغام کنیم و به یه راهحل با پیچیدگی $O(\alpha(n))$ برسیم.
پشتیبانی از فاصله تا نماینده¶
گاهی اوقات تو کاربردهای خاص DSU، لازمه که فاصلهی بین یه گره و لیدر مجموعهش رو هم نگه داری (یعنی طول مسیر توی درخت از گره فعلی تا ریشهی درخت).
اگه از فشردهسازی مسیر استفاده نکنیم، فاصله خیلی ساده میشه تعداد فراخوانیهای بازگشتی. ولی این کارآمد نیست.
با این حال، میشه فشردهسازی مسیر رو انجام داد، اگه فاصله تا والد رو به عنوان اطلاعات اضافی برای هر گره ذخیره کنیم.
توی پیادهسازی، راحتتره که از یه آرایه از pair برای parent[] استفاده کنیم و تابع find_set هم حالا دو تا عدد برگردونه: لیدر مجموعه و فاصله تا اون.
void make_set(int v) {
parent[v] = make_pair(v, 0);
rank[v] = 0;
}
pair<int, int> find_set(int v) {
if (v != parent[v].first) {
int len = parent[v].second;
parent[v] = find_set(parent[v].first);
parent[v].second += len;
}
return parent[v];
}
void union_sets(int a, int b) {
a = find_set(a).first;
b = find_set(b).first;
if (a != b) {
if (rank[a] < rank[b])
swap(a, b);
parent[b] = make_pair(a, 1);
if (rank[a] == rank[b])
rank[a]++;
}
}
پشتیبانی از زوجیت طول مسیر / بررسی دو بخشی بودن به صورت آنلاین¶
همونطور که میتونیم طول مسیر تا لیدر رو حساب کنیم، میتونیم زوجیت طول مسیر رو هم نگه داریم. چرا این کاربرد یه پاراگراف جدا داره؟
نیاز به ذخیرهی زوجیت مسیر توی این مسئلهی جالب پیش میاد: اولش یه گراف خالی بهمون داده میشه، میتونیم بهش یال اضافه کنیم، و باید به پرسوجوهایی مثل این جواب بدیم: "آیا مؤلفه همبندیای که این رأس توش هست، دو بخشی است؟"
برای حل این مسئله، یه DSU برای ذخیره کردن مؤلفهها میسازیم و زوجیت مسیر تا لیدر رو برای هر رأس ذخیره میکنیم. اینطوری میتونیم سریع چک کنیم که آیا اضافه کردن یه یال، خاصیت دو بخشی بودن رو خراب میکنه یا نه: یعنی اگه دو سر یال توی یه مؤلفه همبندی باشن و فاصلهشون تا لیدر زوجیت یکسانی داشته باشه، اضافه کردن این یال یه دور به طول فرد ایجاد میکنه و اون مؤلفه دیگه دو بخشی نخواهد بود.
تنها چالشی که داریم، محاسبهی زوجیت توی متد union_find هست.
اگه یال $(a, b)$ رو اضافه کنیم که دو تا مؤلفه همبندی رو به هم وصل میکنه، موقع اتصال یه درخت به اون یکی باید زوجیت رو تنظیم کنیم.
بیا یه فرمول برای محاسبهی زوجیتی که به لیدر مجموعهی متصلشونده اختصاص پیدا میکنه، در بیاریم. فرض کن $x$ زوجیت طول مسیر از رأس $a$ تا لیدرش $A$ باشه، و $y$ زوجیت طول مسیر از رأس $b$ تا لیدرش $B$ باشه، و $t$ زوجیت مورد نظری باشه که باید بعد از ادغام به $B$ بدیم. مسیر از سه بخش تشکیل شده: از $B$ به $b$، از $b$ به $a$ که با یه یال وصل شدن و زوجیتش $1$ هست، و از $a$ به $A$. پس به این فرمول میرسیم (علامت $\oplus$ همون عملیات XOR هست):
بنابراین مهم نیست چند تا ادغام انجام میدیم، زوجیت یالها از یه لیدر به اون یکی منتقل میشه.
اینم پیادهسازی DSU که از زوجیت پشتیبانی میکنه. مثل بخش قبل، از pair برای ذخیرهی والد و زوجیت استفاده میکنیم. علاوه بر این، برای هر مجموعه توی آرایهی bipartite[] ذخیره میکنیم که آیا هنوز دو بخشی هست یا نه.
void make_set(int v) {
parent[v] = make_pair(v, 0);
rank[v] = 0;
bipartite[v] = true;
}
pair<int, int> find_set(int v) {
if (v != parent[v].first) {
int parity = parent[v].second;
parent[v] = find_set(parent[v].first);
parent[v].second ^= parity;
}
return parent[v];
}
void add_edge(int a, int b) {
pair<int, int> pa = find_set(a);
a = pa.first;
int x = pa.second;
pair<int, int> pb = find_set(b);
b = pb.first;
int y = pb.second;
if (a == b) {
if (x == y)
bipartite[a] = false;
} else {
if (rank[a] < rank[b])
swap (a, b);
parent[b] = make_pair(a, x^y^1);
bipartite[a] &= bipartite[b];
if (rank[a] == rank[b])
++rank[a];
}
}
bool is_bipartite(int v) {
return bipartite[find_set(v).first];
}
پرسش کمینه بازه (RMQ) به صورت آفلاین در $O(\alpha(n))$ به طور متوسط / ترفند آرپا¶
به ما یه آرایه a[] داده شده و باید کمینهها رو توی بازههای مشخصی از آرایه حساب کنیم.
ایدهی حل این مسئله با DSU اینطوریه:
روی آرایه حرکت میکنیم و وقتی روی عنصر i-ام هستیم، به همهی پرسوجوهای (L, R) که R == i دارن، جواب میدیم.
برای اینکه این کار رو بهینه انجام بدیم، یه DSU با استفاده از i عنصر اول و با این ساختار نگه میداریم: والد هر عنصر، عنصر کوچکتر بعدی در سمت راستشه.
اونوقت با این ساختار، جواب یه پرسوجو میشه a[find_set(L)]، یعنی کوچیکترین عدد در سمت راست L.
این روش مشخصه که فقط به صورت آفلاین کار میکنه، یعنی وقتی که همهی پرسوجوها رو از قبل بدونیم.
به راحتی میشه دید که میتونیم از فشردهسازی مسیر استفاده کنیم. و همچنین میتونیم از ادغام بر اساس رتبه استفاده کنیم، اگه لیدر واقعی رو توی یه آرایهی جداگانه ذخیره کنیم.
struct Query {
int L, R, idx;
};
vector<int> answer;
vector<vector<Query>> container;
container[i] شامل همهی پرسوجوهایی میشه که R == i دارن.
stack<int> s;
for (int i = 0; i < n; i++) {
while (!s.empty() && a[s.top()] > a[i]) {
parent[s.top()] = i;
s.pop();
}
s.push(i);
for (Query q : container[i]) {
answer[q.idx] = a[find_set(q.L)];
}
}
امروزه این الگوریتم به اسم ترفند آرپا شناخته میشه. این اسم از امیررضا پورآخوان گرفته شده که به طور مستقل این تکنیک رو کشف و معروف کرد. هرچند این الگوریتم قبل از کشف ایشون هم وجود داشته.
کوچکترین جد مشترک (LCA) به صورت آفلاین در $O(\alpha(n))$ به طور متوسط¶
الگوریتم پیدا کردن LCA توی مقالهی کوچکترین جد مشترک - الگوریتم آفلاین تارجان بحث شده. این الگوریتم به خاطر سادگیاش (مخصوصاً در مقایسه با الگوریتمهای بهینهای مثل الگوریتم Farach-Colton و Bender) با بقیهی الگوریتمهای LCA مقایسهی خوبی داره.
ذخیره DSU به طور صریح در یک لیست مجموعه / کاربردهای این ایده هنگام ادغام ساختمان دادههای مختلف¶
یکی از راههای جایگزین برای ذخیره کردن DSU، اینه که هر مجموعه رو به شکل یه لیست صریح از عناصرش نگه داریم. همزمان، هر عنصر هم یه ارجاع به لیدر مجموعهاش رو ذخیره میکنه.
در نگاه اول این یه ساختمان دادهی ناکارآمد به نظر میرسه: برای ادغام دو تا مجموعه، باید یه لیست رو به ته لیست دیگه اضافه کنیم و لیدر همهی عناصر یکی از لیستها رو آپدیت کنیم.
اما، معلوم میشه که استفاده از یه هیوریستیک وزنی (شبیه ادغام بر اساس اندازه) میتونه پیچیدگی مجانبی رو به شکل قابل توجهی کم کنه: $O(m + n \log n)$ برای انجام $m$ پرسوجو روی $n$ عنصر.
منظور از هیوریستیک وزنی اینه که ما همیشه مجموعهی کوچکتر رو به مجموعهی بزرگتر اضافه میکنیم.
اضافه کردن یه مجموعه به دیگری خیلی راحت توی union_sets پیادهسازی میشه و زمانی متناسب با اندازهی مجموعهی اضافهشونده میبره.
و پیدا کردن لیدر توی find_set با این روش ذخیرهسازی، $O(1)$ طول میکشه.
بیا پیچیدگی زمانی $O(m + n \log n)$ رو برای اجرای $m$ پرسوجو اثبات کنیم.
یه عنصر دلخواه $x$ رو در نظر بگیر و تعداد دفعاتی که توی عملیات ادغام union_sets بهش دست زده شده رو بشمار.
وقتی عنصر $x$ برای اولین بار لمس میشه، اندازهی مجموعهی جدید حداقل $2$ میشه.
وقتی برای بار دوم لمس میشه، مجموعهی حاصل اندازهای حداقل $4$ خواهد داشت، چون مجموعهی کوچیکتر به بزرگتر اضافه میشه.
و همینطور الی آخر.
این یعنی $x$ حداکثر میتونه توی $\log n$ عملیات ادغام جابجا بشه.
بنابراین، جمع روی همهی رأسها به ما $O(n \log n)$ به علاوهی $O(1)$ برای هر درخواست رو میده.
اینم یه پیادهسازی:
vector<int> lst[MAXN];
int parent[MAXN];
void make_set(int v) {
lst[v] = vector<int>(1, v);
parent[v] = v;
}
int find_set(int v) {
return parent[v];
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (lst[a].size() < lst[b].size())
swap(a, b);
while (!lst[b].empty()) {
int v = lst[b].back();
lst[b].pop_back();
parent[v] = a;
lst[a].push_back (v);
}
}
}
این ایدهی اضافه کردن بخش کوچیکتر به بخش بزرگتر میتونه تو خیلی از راهحلهایی که هیچ ربطی به DSU ندارن هم استفاده بشه.
مثلاً، این مسئله رو در نظر بگیر: یه درخت بهمون دادن، هر برگ یه عدد بهش اختصاص داده شده (یه عدد ممکنه چند بار تو برگهای مختلف بیاد). میخوایم تعداد اعداد مختلف توی زیردرخت رو برای هر گره درخت حساب کنیم.
با اعمال همین ایده به این مسئله، میتونیم به این راهحل برسیم:
میتونیم یه DFS پیادهسازی کنیم که یه اشارهگر به یه set از اعداد صحیح برگردونه – یعنی لیست اعداد توی اون زیردرخت.
بعد برای به دست آوردن جواب برای گره فعلی (مگر اینکه برگ باشه)، DFS رو برای همهی بچههاش صدا میزنیم و همهی setهای دریافتی رو با هم ادغام میکنیم.
اندازهی set حاصل، جواب برای گره فعلی خواهد بود.
برای ادغام بهینهی چند تا set، همون دستوری که بالا گفتیم رو اعمال میکنیم:
setها رو با اضافه کردن setهای کوچیکتر به بزرگترها ادغام میکنیم.
در نهایت، به یه راهحل $O(n \log^2 n)$ میرسیم، چون یه عدد فقط حداکثر $O(\log n)$ بار به یه set اضافه میشه.
ذخیره DSU با نگهداری یک ساختار درختی واضح / یافتن پل به صورت آنلاین در $O(\alpha(n))$ به طور متوسط¶
یکی از قویترین کاربردهای DSU اینه که بهت اجازه میده اون رو هم به صورت درختهای فشرده و هم غیرفشرده ذخیره کنی. فرم فشرده میتونه برای ادغام درختها و چک کردن اینکه آیا دو تا گره توی یه درخت هستن استفاده بشه، و فرم غیرفشرده میتونه – مثلاً – برای جستجوی مسیر بین دو تا گره یا پیمایشهای دیگه روی ساختار درخت استفاده بشه.
توی پیادهسازی، این یعنی علاوه بر آرایهی والد فشردهی parent[]، باید آرایهی والد غیرفشردهی real_parent[] رو هم نگه داریم.
مشخصه که نگه داشتن این آرایهی اضافی، پیچیدگی رو بدتر نمیکنه:
تغییرات توی اون فقط موقعی رخ میده که دو تا درخت رو ادغام میکنیم، و فقط روی یه عنصر.
از طرف دیگه، توی کاربردهای عملی، ما اغلب نیاز داریم که درختها رو با استفاده از یه یال مشخص به هم وصل کنیم، نه با استفاده از دو تا گره ریشه. این یعنی چارهای جز ریشهدار کردن مجدد یکی از درختها نداریم (یعنی یکی از سرهای یال رو به عنوان ریشهی جدید درخت قرار بدیم).
در نگاه اول به نظر میرسه که این ریشهدار کردن مجدد خیلی پرهزینهست و پیچیدگی زمانی رو به شدت بدتر میکنه.
در واقع، برای ریشهدار کردن یه درخت در رأس $v$، باید از اون رأس تا ریشهی قدیمی بریم و جهتها رو توی parent[] و real_parent[] برای همهی گرههای اون مسیر عوض کنیم.
اما در واقعیت اونقدرها هم بد نیست. میتونیم شبیه ایدههای بخشهای قبلی، درخت کوچکتر از دو تا درخت رو ریشهدار کنیم و به طور میانگین به پیچیدگی $O(\log n)$ برسیم.
جزئیات بیشتر (شامل اثبات پیچیدگی زمانی) رو میتونی توی مقالهی یافتن پلها به صورت آنلاین پیدا کنی.
نگاهی به تاریخچه¶
ساختمان دادهی DSU از خیلی وقت پیش شناخته شده.
ظاهراً این روش ذخیرهسازی به شکل جنگلی از درختان اولین بار توسط گالر و فیشر در سال ۱۹۶۴ توصیف شد (Galler, Fisher, "An Improved Equivalence Algorithm)، ولی تحلیل کامل پیچیدگی زمانیش خیلی دیرتر انجام شد.
بهینهسازیهای فشردهسازی مسیر و ادغام بر اساس رتبه توسط مکایلروی و موریس و به طور مستقل توسط تریتر توسعه پیدا کرد.
هاپکرافت و اولمن در سال ۱۹۷۳ پیچیدگی زمانی $O(\log^\star n)$ رو نشون دادن (Hopcroft, Ullman "Set-merging algorithms") - اینجا $\log^\star$ لگاریتم مکرر هست (این یه تابع با رشد خیلی کنده، ولی هنوز به کندی معکوس تابع آکرمن نیست).
برای اولین بار، ارزیابی $O(\alpha(n))$ در سال ۱۹۷۵ توسط تارجان نشون داده شد (Tarjan "Efficiency of a Good But Not Linear Set Union Algorithm"). بعدها در سال ۱۹۸۵، او به همراه لیوون، تحلیلهای پیچیدگی متعددی رو برای چندین روش رتبهبندی مختلف و راههای فشردهسازی مسیر منتشر کردن (Tarjan, Leeuwen "Worst-case Analysis of Set Union Algorithms").
و بالاخره در سال ۱۹۸۹، فردمن و ساکس ثابت کردن که توی مدل محاسباتی پذیرفته شده، هر الگوریتمی برای مسئلهی مجموعههای مجزا باید به طور متوسط حداقل در زمان $O(\alpha(n))$ کار کنه (Fredman, Saks, "The cell probe complexity of dynamic data structures").